I feel like the big standard that students learn in 2nd grade is 3 digit addition strategies. During the school year we set the foundation with math facts and place value concepts so that students can be successful with three digit addition strategies. And to be honest, they are some of my favorite lessons in 2nd grade! I’ve learned that for students to be successful with strategies for 3-digit addition, you need to help them see how place value is involved and then help them see the patterns that are needed to do the strategies.

 

So today, I thought I would share the 4 different 3-digit addition strategies I teach in my 2nd grade classroom including the place value concepts that directly correlate with these strategies and the patterns students need to notice for each of these strategies.

 

But before we get started, it’s important to know that students do much better on these 3-digit addition strategies when they are fluent with their basic addition and subtraction math facts. I have a free workbook to help you get your students to math fact fluency: The 7 Steps to Ensure Math Fact Fluency. Download your free copy here.

Also… If you’re a parent who has a child struggling with math, you’ve got to check out Learner. Learner is an online tutoring platform that sets students up for success. To get started take a short quiz about your child’s needs. Then Learner’s Success Management Team reviews that and matches your child with the perfect tutor. Get your $25 trial here.

 

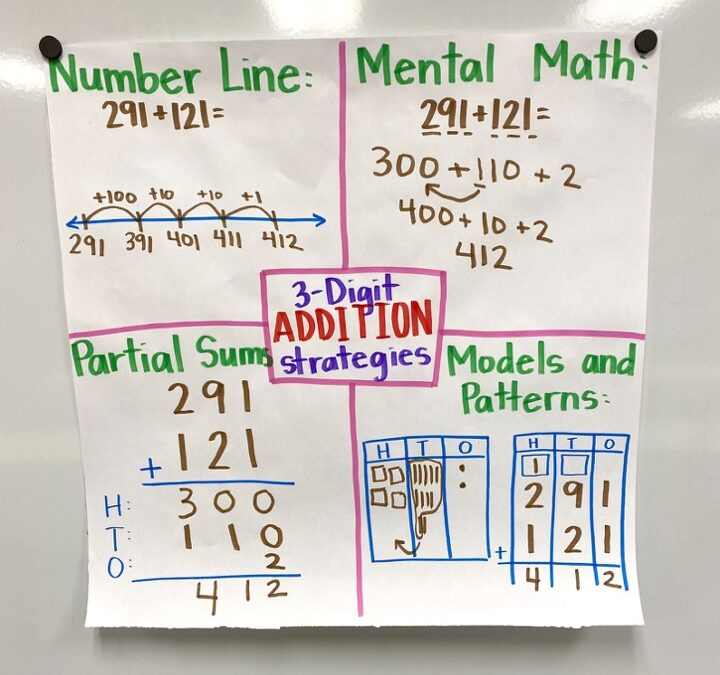
3-Digit Addition Strategies

 

The 3-digit addition strategies I teach my students are the open number line strategy, mental math or the expanded form strategy, partial sums, and regrouping or the standard algorithm.

 

 

Open Number Line 3-Digit Addition Strategy

 

With this strategy, students make jumps of hundreds, tens, and ones on an open number line to add the two numbers. Let’s look at an example with the equation 356 + 223. For students to solve this equation, they would start by making a little “tick” on the left side of the open number line and label it 356 underneath.

 

 

Then they look at how many hundreds are in the number they are adding. In this case, students make 2 one hundred jumps. They label these jumps with a “+100” up above their jumps. Down below they are going to add 100 to their starting number. So they would write “456” and “556” underneath.

 

Then they look at how many tens are in the number they are adding and make that many jumps. For this example, they make 2 tens jumps and label them “+10” up above. Then they need to write the numbers underneath where they add 10, so they write “566” and “576.”

 

And finally, they look at how many ones are in the number they are adding. There are 3 ones in 223 so students then make three jumps and label them “+1” up above. Down below they add the numbers where they add 1, so they write “576, 577, and 578.” The last number they write underneath is their answer.

 

Now let’s talk about the place value concepts students need to know before you teach this strategy. Students need to know what the hundreds place is, the tens place is, and the ones place. They need to know that the first 2 in 223 doesn’t just mean 2, it means 200. I have a blog post where I share exactly how to teach this concept to your students. Read it here: Place Value Standards: How to Best Teach Them to 2nd Grade Students

 

For students to do this 3-digit addition strategy they need to know important patterns. They need to do the mental math involved in adding 100 to a number, 10 to a number, and 1 to a number. There is also what I call a “special 10 pattern.” This is when you add 10 to a 3-digit number when there is a 9 in the tens place.

 

These patterns are so important, I actually teach a whole lesson on them the day before my lesson on the open number line strategy.

 

I have a blog post going into detail with that lesson and my open number line strategy. It shares what I do for direct instruction, guided practice, independent practice, extra practice, and assessment. Read it here: Open Number Line Strategy: How to Best Teach it Using 3-Digit Numbers

 

Find all of my resources to teach the open number line strategy in my money-saving bundle here.

 

Mental Math 3-Digit Addition Strategy

 

This mental math strategy has students add the hundreds, tens, and ones together to get the expanded form equation. Then students may need to move around a hundred or a ten for the equation to truly be in expanded form. Then students can just put the number in standard form to get the answer.

 

Let’s look at an example for this to make a little more sense. If we had the equation 425+293, students would first add the hundreds to get 600. Then they would add the tens to get 110. Then they would add the ones to get 8. They put those numbers in the new equation to look like this 600+110+8. This almost looks like expanded form, but it is not. There is an extra hundred in the tens number, so you give that to the hundreds to get the equation 700+10+8. Then students can easily put that equation in standard form to get the answer, 718.

 

 

For students to be successful with this 3-digit addition strategy, they need to know the place value concepts of expanded form and standard form. They also need to know how to be flexible when making equations for a 3-digit number. I teach these lessons in our place value unit. Learn how to teach these lessons in this blog post here.

 

For students to do this strategy mentally, they need to pick up on patterns when they add hundreds, tens, and ones. They also need scaffolding where little by little you take away supports. Learn exactly how I do that here in this blog post: Mental Math Addition Practice: How to Actually Get Students to Add 3-Digit Number Mentally

 

In this blog post, I also share what I do for direct instruction, guided practice, independent practice, extra practice, and assessment for this strategy. Read it here.

 

Find all of my resources for teaching this strategy here in this money-saving bundle.

 

Partial Sums 3-Digit Addition Strategy

 

For partial sums, students add the hundreds, the tens, and the ones, and then line these numbers up according to place value. Then they add going straight down to get the answer. 

 

Let’s look at an example for this to make a little more sense. If we have the equation 352+139, you add the hundreds first to get 400 and write that underneath the equals line. Then you add the tens to get 80. You put this under the 400 and line it up according to place value. And then you add the ones to get 11 and put that underneath the 80 making sure to line it up according to place value. Since you have everything lined up, you can get your answer by adding those numbers by going straight down. I like to start with the ones, 0+0+1=1. Then the tens, 0+8+1=9, and then finally the hundreds, 4+0+0=4. So you get the number 491 as your answer.

 

 

This is one of my students’ favorite 3-digit addition strategies because they love the easy equations they get then they add going straight down.

 

For this strategy, students need to know that where the digit placed in the 3-digit number determines its value. The 3 in 352 doesn’t mean 3, it means 3 hundreds or 300. When they understand this it will also help students line up the numbers according to place value.

 

I also like to teach students the pattern of adding tens together. I first use base tens blocks to do this. I show them 8 ten rods and add 4 ten rods to it. Then we count by 10s to get to the answer of 120. I continue this until students see the pattern that when we add tens, we count up how many tens and then add a zero at the end.

 

Learn exactly how I teach the partial sums strategy here in this blog post: Partial Sums Addition Method: How to Best Teach This Strategy to Second Grade Students

 

In this blog post you’ll learn what to do for direct instruction, guided practice, independent practice, extra practice, and assessment. Read it here.

 

Find all the resources I use to teach the partial sums strategy in this money-saving bundle here.

 

Regrouping 3-Digit Addition Strategy

 

For regrouping, I eventually get students while they line up the numbers and start with the ones to add. If the ones make 10 or more, they regroup. Then they move over to add the tens. If there are 10 or more tens, they regroup. And then to find the answer, they add the hundreds together.

 

But it takes some time to teach this 3-digit addition strategy so that students build understanding on what it means to regroup instead of just following rote rules. To do this I first have students solve these equations by drawing base ten blocks. I have them do this in a hundreds, tens, and ones chart. They circle 10 ones or 10 tens when they need to regroup and draw an arrow to the next column and draw in that ten rod or hundreds block. This helps students see why regrouping works.

 

Then the next day we do a lesson where I still have students draw models to solve, but they also line up the numbers to show what they are doing with the pictures.

 

 

After that, I have a lesson where I help students see patterns that they can apply with just lining up the numbers to solve.

 

These patterns include that when students add the ones together, if the sum is a single digit they just write it below. If it’s 10 or more, the 1 ten goes in the tens place to be added with the other tens. I often say to my students something like this, “5+7=12. 12 is a group of ten and 2 ones left over. We put that group of ten over with the other tens, and we write the 2 ones down below.”

 

When you teach regrouping lessons in this way, things fall into place for students. They don’t struggle with the steps because they have seen the mechanics of it all. They really do master regrouping!

 

Learn more about each of these lessons here in this blog post: How to Best Teach The Regrouping Method With 3-Digit Addition

 

Find all of the resources I use to teach the regrouping method in this money-saving bundle here.

 

3-Digit Addition Printable Worksheets

 

As I am teaching each of these 3-digit addition strategies, I like to provide scaffolding along the way. Even before these lessons, I teach my place value lessons. Learn about these lessons in this blog post here. Then right before I teach the new strategy, I review the place value concept that directly correlates with the strategy. Find the resources I use to do this here.

 

I start students off with worksheets that have different features that help guide students. Then I give them worksheets that slowly take away those features so that students can do these different 3-digit addition strategies with a little less guidance. Soon they can be successful with the strategies!

 

 

Let me give you an example with the mental math strategy. I start by giving students worksheets that have boxes where they write the equations to add the hundreds together, the tens together, and the ones together. Then there are equation frames below to help students get the equations to expanded form so that they can get to the answer. Next, I’ll give a worksheet that doesn’t have the boxes. Students have to do that in their heads, but there still are the equation frames for students to use. Then finally, I give them worksheets without the boxes or equation frames. They just solve the equations mentally.

 

Find these scaffold worksheets to teach 3-digit addition strategies here.

 

I hope that from reading this blog post you have seen the importance of relating each 3-digit addition strategy to its corresponding place value concept as well as helping students see patterns in the strategies to help them. When you teach 3-digit addition strategies in this way, your students can be successful with them!

 

Need tips with 2-digit addition and subtraction strategies? Check out these blog posts:

 

2-Digit Addition Strategies That Work

 

How to Teach Those Tricky 2-Digit Subtraction Strategies